Aufgabe B 2
Zwei Flugzeuge F1 und F2 bewegen sich geradlinig mit jeweils konstanter
Geschwindigkeit über dem offenen Meer. In einem Koordinatensystem beschreibt
dabei die x1x2-Ebene die Meeresoberfläche.
Die Beobachtung der Flugzeuge beginnt um 14.00 Uhr.
Die Flugbahn von F1 wird beschrieben durch die Gleichung
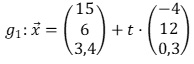(t in Minuten nach Beobachtungsbeginn).
a) Berechnen Sie die Geschwindigkeit von F1 in km/min.
Bestimmen Sie den Zeitpunkt, zu dem F1 eine Höhe von 4,9 km erreicht.
Berechnen Sie die Weite des Winkels, mit dem das Flugzeug F2 steigt.
(3 VP)
b) Die Flugbahnen von F1 und F2 schneiden sich.Aus Sicherheitsgründen müssen die Zeitpunkte, zu denen die Flugzeuge den Schnittpunkt ihrer Flugbahnen durchfliegen, mindestens eine Minute auseinander liegen.
Prüfen Sie, ob diese Bedingung erfüllt ist.
(3 VP)
c) Die Position eines Ballons wird durch den Punkt B(6|43|4,3) beschrieben.Bestimmen Sie einen Zeitpunkt t0, zu dem beide Flugzeuge denselben Abstand vom Ballon haben.
Die Punkte auf der Meeresoberfläche, die zum Zeitpunkt t0 ebenfalls von beiden Flugzeugen gleich weit entfernt sind, liegen auf einer Geraden.
Beschreiben Sie ein Verfahren, mit dem man eine Gleichung dieser Geraden bestimmen kann.
(4 VP)